
So the main reason is because it's a quadrilateral instead of a triangle. This would not be, um this is why this doesn't work. This is the most frequently used method for proving triangle similarity and is therefore the most important. The AA theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
Angle-Angle (AA) Triangle Similarity Theorem.You can use the AA (Angle-Angle) method to prove that triangles are similar. 
We don't have congruent angles for the others in the same order. The Explore suggests the following theorem for determining whether two triangles are similar. The SSS Similarity Theorem is used when the corresponding. So that that's one example where you have the bottom angles are your congruent angles, but then we don't have similar. The AA Similarity Postulate is used when two pairs of congruent angles of two triangles are given. I'm calling this like the bottom angles and not have similar figures.
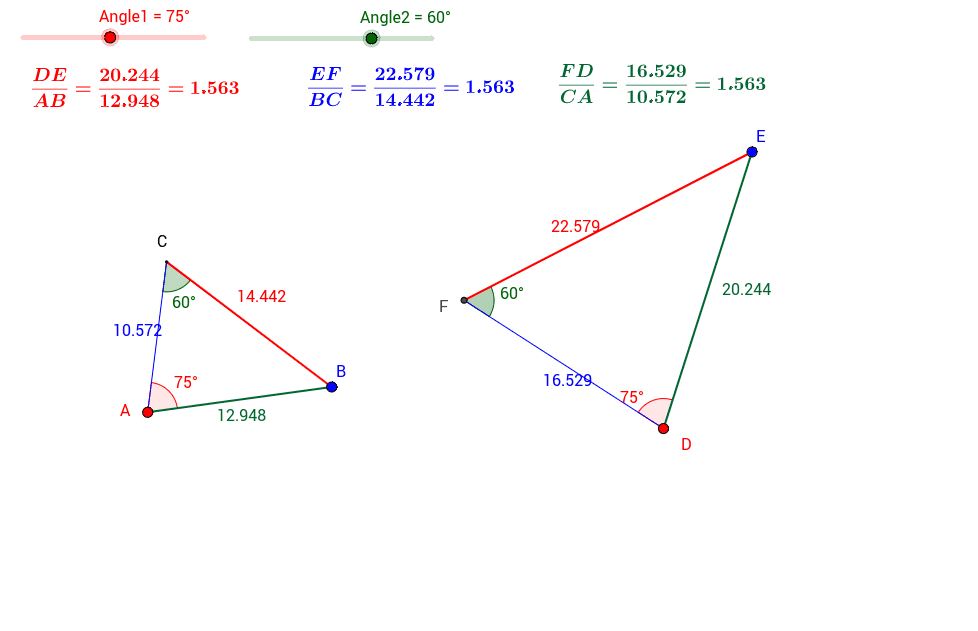
The Angle-Angle (AA) criterion for similarity of two triangles states that If two angles of one triangle are. Um, so, like, you could have, uh, two angles. AA Similarity Criterion for Two Triangles.

Like if the third angle in the fourth angle would be something that would make a similar figure because the other two angles just have to add up Thio, whatever. And whatever the I want to say compliment or supplement is. If you only know two angles and the other two angles could be anything that adds up to. The mathematical definition for similar triangles states that the. Okay, So for these two shapes, uh, it's kind of obvious what the error is, but for the a similarity, Um, here, um, it deals with that theory on deals with triangles just because knowing two angles, you know what the third angle is? Eso for quadrilateral. The AA Criterion When you have two triangles where one is a smaller version of the other, you are looking at two similar triangles.


 0 kommentar(er)
0 kommentar(er)
